Консенсус в распределенных системах

Распределенные системы существуют по двум основным причинам, причем обе из них стали крайне актуальны в последнее десятилетие. Во-первых, объемы хранимых и обрабатываемых данных постоянно растут и для многих систем уже давно не умещаются на одном физическом носителе. Во-вторых, этих носителей настолько много, что каждый год выходят из строя тысячи из них. Поэтому, чтобы избежать потери информации, необходимо использовать репликацию, то есть хранить копии одних и тех же данных на нескольких устройствах. Это позволит избежать единой точки отказа, так как при выходе из строя одного узла системы, можно будет продолжить работу с другим.

Создание отказоустойчивой распределенной системы — сложная алгоритмическая и инженерная задача. В этой статье мы сделаем акцент на теоретической части этой проблемы. Мы опишем ее в общем виде, рассмотрим задачу консенсуса, которая напрямую связана с исходной и познакомимся с подходами, используемыми для решения этой задачи на примере двух популярных алгоритмов консенсуса. Этот пост является вводным в область распределенных систем, поэтому я не буду доказывать теоремы и в точности описывать протоколы консенсуса, тем не менее ссылки на статьи будут приведены.

На написание этого поста меня вдохновили лекции Романа Липовского, который прочитал курс по распределенным алгоритмам в CS клубе. Все видео лекций доступны на странице курса.

Модель распределенной системы

Начнем с того, что формализуем распределенную систему и мир, в котором она работает. Система представляет собой набор узлов и связей между ними. По этим связям узлы могут обмениваться сообщениями. Вне системы существуют пользователи, которые могут отправлять запросы к различным узлам системы и ожидать от них ответов.

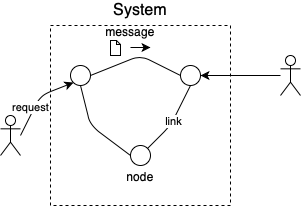
Обсудим характеристики нашей модели:

1. Узлы могут работать с произвольной скоростью. В реальности, как правило, мы не можем управлять сборкой мусора или быть уверенными, что нужное значение есть в кэше и т.д. Поэтому отсутствие ограничений на время работы узлов выглядит логичным.
2. Время передачи сообщения от узла к узлу не ограничено сверху по времени. В жизни это кажется слишком сильным условием: обычно у нас есть гарантии, что пакет будет доставлен в разумные сроки. Тем не менее, мы принимаем эту модель (она называется асинхронной), так как в случае построения корректного алгоритма в такой модели, можно быть уверенным, что он будет работать и в реальной жизни.
3. Узлы подвержены только простым отказам. Простой отказ означает прекращение работы узла. Мы не будем рассматривать византийские отказы, то есть случаи, когда реплики могут перестать выполнять протокол и вести себя как им вздумается. Кроме того, наша модель допускает partitions — ситуации, когда часть реплик не может связаться с другими, но при этом и та и другая группа может принимать запросы пользователей.
4. Узлы изолированны. Мы предполагаем, что отказ одного узла никак не влияет на другие. Это предположение не всегда работает на практике, так как реплики могут находиться в одной стойке (отказ коммутатора сломает все узлы в стойке) или в одном дата центре (пожар или сбой в питании) и т.д.

Задача репликации лога

Теперь, когда модель определена, мы можем решать в этой модели различные задачи. Поставим достаточно общую задачу, которую решают в том или ином виде большинство современных распределенных систем. Состояние узла системы изменяется под действием некоторого конечного автомата. Пользователь отправляет команду на один из узлов, который делится этой командой с остальными репликами и команда применяется, в результате чего узел переходит в новое состояние. Изначально все узлы находятся в одинаковом состоянии. Необходим алгоритм, с помощью которого команды на репликах будут выполняться в одинаковом порядке, за счет чего в конце концов узлы будут находиться в одном и том же состоянии.

В промышленных системах команды на каждой из реплик записываются в лог. И задача сводится к тому, чтобы обеспечить одинаковый порядок команд в каждом из логов узлов. Как только реплика уверена, что команда зафиксирована на некотором месте (то есть в конечном счете на каждой из доступных реплик она окажется в этой же позиции), узел применяет команду к своему конечному автомату. Например, если система — распределенное key-value хранилище, это может быть команда записи значения по ключу.

Так как мы строим отказоустойчивую систему, она должна переживать некоторое число отказов (какое именно, мы обсудим чуть позже). Переживать — означает продолжать корректно работать на оставшихся репликах и отвечать на запросы клиентов. Кроме того, если число отказов стало слишком велико, то мы хотим, чтобы система просто перестала отвечать клиенту на его запросы, но при этом оставалась в корректном состоянии. Тогда при восстановлении сломанных узлов, система сможет продолжить работу.

Консенсус и теорема FLP

Описанная задача сводится к другой, значительно более простой по своему описанию, но при этом столь же трудной по своей сути. Она называется задачей консенсуса. По условию этой задачи, каждому из узлов подается на вход некоторое свое значение. Необходимо, чтобы в результате алгоритма все узлы выбрали одинаковое значение (обязательно одно из тех, что было подано на входы) и перешли в состояние выбрано. При этом алгоритм должен завершаться.

Докажем, что эта задача невыполнима, если среди исходных n узлов произойдет не менее n/2 отказов. Пойдем от обратного. Пусть такой алгоритм существует. Рассмотрим три различных выполнения этого алгоритма на одинаковом наборе узлов:

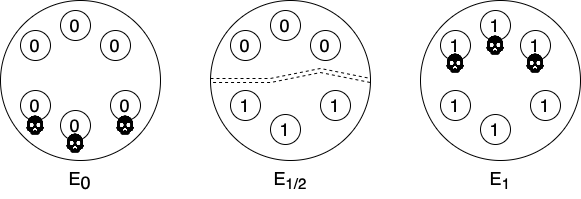
В выполнении E₀ всем узлам на вход передан ноль. При этом нижняя половина узлов вышла из строя. Аналогично, в E₁ у всех узлов на входах единицы, а из строя вышла верхняя половина. Так как по предположению наш алгоритм консенсуса корректен, эти отказы не помешают узлам выбрать значения 0 и 1 соответственно. Теперь рассмотрим выполнение E_1/2 в котором верхней половине передано значение 0, а нижней — 1. При этом, отказов не произошло, но между узлами возник partition, т.е. узлы верхней половины не подозревают о существовании узлов из нижней и наоборот. В результате узлы обеих половин не отличают данное выполнение от E₀ и E₁ соответственно. Следовательно выберут разные значения, что противоречит корректности нашего алгоритма.

На основе этих рассуждений наша распределенная система должна продолжать свою работу, если в ней менее половины отказов. Кроме того, мы можем прийти к выводу, что логичнее использовать нечетное число реплик. Это следует из того, что и при 2k-1 и при 2k репликах, число отказов которое сможет пережить система равно k. Нет смысла в таком случае увеличивать число узлов, а значит и количество коммуникаций между ними.

Но есть и еще один доказанный факт, который приводит к мысли, что задача консенсуса совсем плохо ладит с отказами. Теорема FLP (Фишер-Линч-Патерсон) говорит о том, что для детерминированного алгоритма консенсуса достаточно хотя бы одного отказа, чтобы существовало исполнение, в котором алгоритм не будет завершен. Доказательство. Тем не менее, в реальных системах есть различные механики (например, тайм-ауты случайной длительности), которые позволяют уйти от детерминизма алгоритма и как результат от отсутствия прогресса в системе.

Кворумы

Я не стану вдаваться в подробности работы алгоритмов консенсуса, но расскажу про одну из важнейших техник, которая используется в распределенных алгоритмах. Формально, про кворум можно почитать здесь, я же расскажу про кворум простого большинства. Таким кворумом является любое большинство узлов системы. Любой из классических алгоритмов консенсуса используют кворумы для гарантии сохранения информации на выживших устройствах.

Как мы уже доказали, консенсус не будет работать, если отказов в системе больше половины. Это число напрямую связано с кворумами. Почти любой шаг алгоритма консенсуса считается завершенным, только когда набрал кворум сообщений-подтверждений. При этом, если отказов стало больше половины, то кворум просто не наберется, и система не будет отвечать клиенту, пока это не произойдет.

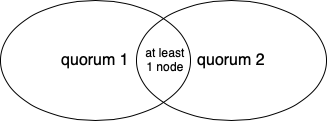
Почему же использование кворумов необходимо? Допустим, реплика решила бы отвечать клиенту без кворума, а сразу применив команду и отправив информацию об этом другим узлам. Но если этот узел отрезан от других из-за partition, то эта информация до них не дойдет, и состояние системы станет неконсистентным. За счет того, что каждый шаг алгоритма подтвержден кворумом реплик, можно быть уверенным, что на следующем шаге в кворуме окажется хотя бы один узел, который знал о завершении предыдущего шага и сможет донести эту информацию до остальных. Это возможно благодаря тому, что любые два кворума имеют непустое пересечение.

Алгоритм MultiPaxos

В 1990 году Лесли Лампорт написал своеобразную статью про выдуманный древнегреческий остров Paxos, в которой отождествлял парламент и распределенную систему, членов парламента и реплики, свод законов и лог с командами. В этой статье много юмора и забавных аналогий между ситуациями в исполнении распределенной системы и жизни выдуманных министров. Также в ней Лампорт описал алгоритм консенсуса, но несмотря на это рецензенты не оценили подачу статьи и она не была опубликована аж до 1998 года.

Предложенный алгоритм консенсуса, который так и называется Paxos, содержит совсем немного кода и не кажется сложным (псевдокод), но многими признается как совершенно неинтуитивный. На основе этого алгоритма Лампорт предложил и решение задачи репликации лога. В простейшем варианте реплика при получении команды от пользователя, предлагает команду в ближайший свободный слот лога и запускает консенсус на этом слоте. В итоге выигравшая команда записывается в этом слоте у каждой из реплик, а проигравшие предлагаются в следующих слотах. Как только команда признана как выбранная, ее можно выполнять и отвечать клиенту. Этот алгоритм был назван MultiPaxos.

Алгоритм RAFT

Этот алгоритм был придуман только лишь в 2014 году. При этом он работает не эффективнее, чем MultiPaxos, поэтому возникает вопрос, зачем нужен еще один алгоритм, решающий ту же задачу. Авторы в начале своей статьи отвечают на этот вопрос. Во-первых, они считают, что подход Лампорта в решении задачи консенсуса в каждом слоте не самый логичный и сложный для восприятия. Они предлагают другой подход, где решают задачу репликации сразу для всего лога. Во-вторых, статья Лампорта, как уже было сказано, про греков. А сам алгоритм MultiPaxos описан только в общих словах и реализовать по нему полноценную репликацию достаточно непросто. Авторы RAFT предоставили полностью описанный протокол, что крайне упрощает реализацию алгоритма.

Сам алгоритм состоит из двух фаз: выбора лидера и непосредственной репликации. Если не вдваться в подробности, то на первой фазе реплики обмениваются сообщениями, чтобы выбрать узел, который будет принимать команды от пользователя. На второй фазе выбранный узел заполняет лог командами и рассылает команды остальным репликам.

Казалось бы, крайне логичное поведение, которое предложил бы любой разработчик не особо знакомый с распределенными алгоритмами. Но все работает так просто, только тогда, когда все в системе идеально. Как только между репликами возникает partition или проблемы в сети и начинают срабатывать тайм-ауты, когда появляется несколько лидеров, тогда становится все намного сложнее. При этом алгоритмы MultiPaxos и RAFT даже в такой ситуации гарантируют корректность системы, хотя и не могут на 100% уберечь от отсутствия прогресса в системе, как и обещает нам теорема FLP.

Заключение

Я не стал описывать алгоритмы консенсуса, потому что тогда статья стала бы далеко не вводной. Если вам необходимо что-либо реплицировать в своей системе, обязательно воспользуйтесь готовой реализацией алгоритма (например, RAFT). Эта задача имеет так много подводных камней, что тут уж точно не стоит выдумывать свой велосипед.

Written on January 12th, 2020 by Alexey Kalina