NP-полные задачи

Программист Вася регулярно встречается на работе с новыми для себя задачами. Он как обычно придумал решение, но в этот раз случилось так, что его алгоритм выполняется слишком долго. Временем нужно дорожить, поэтому Васе досталось от начальства. Эта проблема возникла сразу по двум причинам. Во-первых, наверняка задачу Васи уже кто-то решал, либо она сводится к уже решенной. Во-вторых, он не подумал о сложности выполнения алгоритма. Небольшой анализ предотвратил бы бесполезную трату времени.

Далеко не все задачи можно решить за разумное время. Возможно, наш герой столкнулся именно с такой. Сегодня мы познакомимся с группой задач, которые могут выполняться всю вашу жизнь даже при не очень больших размерах входных данных. Мы разберемся с понятием NP-полноты и временной сложности алгоритмов. И напоследок мы научимся доказывать то, что задача является NP-полной, сузив ее до более простой, но столь же долго решаемой. Зная это, Вася мог бы не тратить время, а объяснить начальству, что от него хотят невозможного.

Машины Тьюринга

Начнем с понятия, на котором строится теория сложности. Машина Тьюринга (МТ). Это всего лишь один из способов описания алгоритмов. Алгоритмы можно описывать на языках высокого уровня, математическими формулами и даже на словах, активно размахивая при этом руками. Тем не менее, машина Тьюринга обладает двумя ключевыми свойствами: она формальна и близка к реальным вычислительным устройствам (читай — компьютерам).

Благодаря формальности машины Тьюринга, можно математически доказывать утверждения об алгоритмах. Например, вывести, что количество операций в сортировке пузырьком квадратично зависит от длины массива. Чуть позже мы встретимся с более неочевидными утверждениями. Так как машина Тьюринга “похожа” на схему работы обычного компьютера, мы можем пользоваться этими утверждениями в работе.

Я уже достаточно сказал о важности машины Тьюринга, но ничего о том, что она из себя представляет. Формально МТ определяется через три объекта: множество символов, множество состояний и правила перехода из одного состояния в другое. Технически же — это бесконечная лента, разделенная на ячейки. По этой ленте движется головка. За каждый шаг машины Тьюринга она может заменить содержимое обозреваемой ячейки, сдвинуться на одну ячейку и изменить состояние машины. Она заканчивает выполнение, когда приходит в конечное состояние (опредлеленное заранее). Результатом выполнения будет слово на ленте.

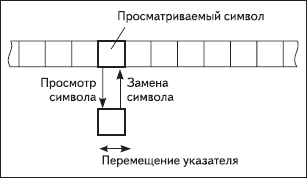
Машина Тьюринга, которую я описал, называется детерминированной. Такое название исходит из того, что каждый шаг машины строго определен. Чтобы пояснить это, определим правила перехода. Они имеют вид: ` q_ia → q_jSb ` . МТ в состоянии ` q_i ` , читающая символ ` a ` , переходит в состояние ` q_j ` , заменяет символ ` a ` на ` b ` и сдвигается на одну ячейку либо остается на месте: ` S = {L, R, \emptyset} ` . В детерминированной машине Тьюринга каждой паре ` (q_i, a) ` соответствует не более одной команды. Недетерминированной называется машина Тьюринга, в которой есть команды вида: ` q_ia → q_jSb, q_ia → q_kSb ` . При выполнении таких команд лента МТ размножается и оставшаяся часть программы выполняется независимо. Если хоть одна из лент пришла в конечное состояние, машина Тьюринга заканчивает выполнение.

Классы сложности

Теперь мы готовы понять, как можно оценивать длительность выполнения алгоритмов. Временной сложностью алгоритма называется функция, которая зависит от длины исходных данных и характеризует число шагов работы алгоритма над этими данными. Мы не зря определили машину Тьюринга, так как оценивать сложность будем именно на ней. Таким образом, длина исходных данных — это число занятых ячеек перед началом выполнения МТ, а шаги работы соответствуют переходам при выполнении МТ.

Вычислить точную оценку трудно и бессмысленно. Для понимания сложности алгоритма достаточно оценить время выполнения с помощью О-символики. Напомню, что функция ` f ` называется О большим от ` g ` , если существует константа ` C ` , такая что ` \abs{f(x)} < C\abs{g(x)} ` для любых ` x ` . Когда мы говорим, что количество операций в сортировке пузырьком — есть квадрат от длины массива, мы имеем ввиду именно О-символику. Нам неважно сколько именно действий нужно выполнить в различных случаях, а достаточно функции, которой можно это число ограничить.

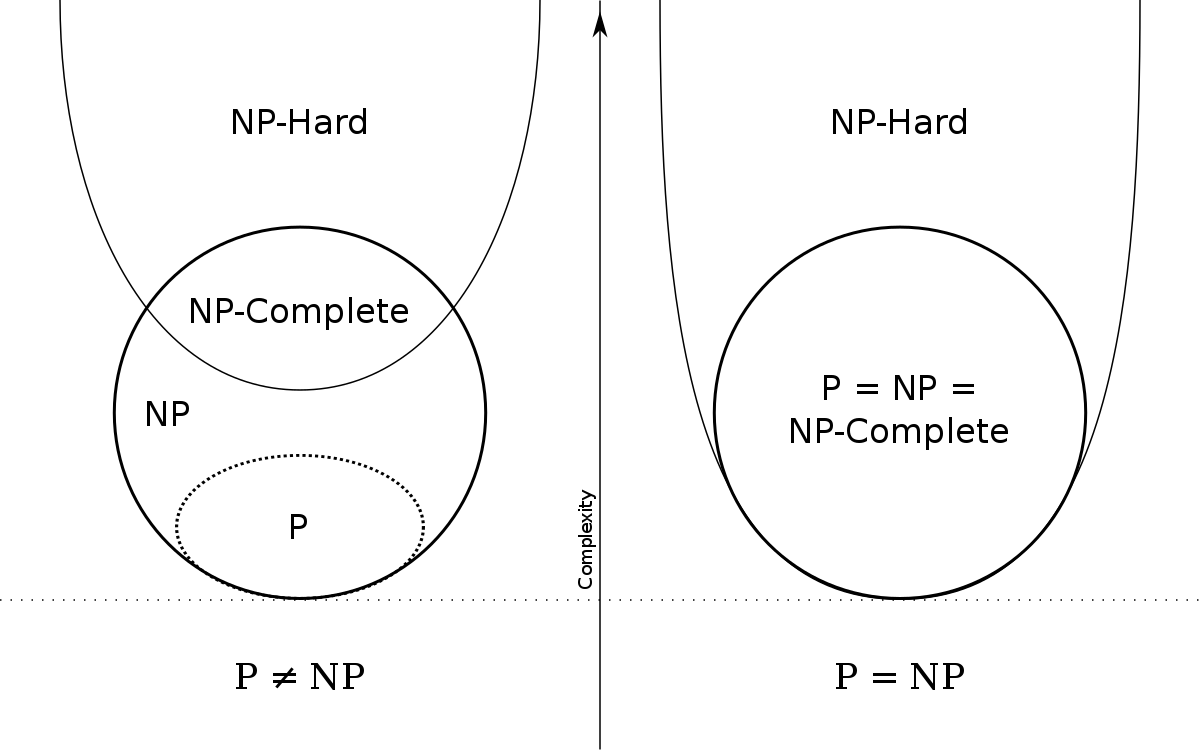
Теперь мы можем говорить об алгоритмах в терминах теории сложности. У нас есть ` O(n\logn), O(n^2), O(2^n) ` и так далее. Мы начали с проблемы Васи и существования программ, которые могут выполняться очень долго. Пришло время разбить алгоритмы на классы, с учетом асимптотики времени их выполнения. Мы остановимся на двух классах, которые называются P и NP. Буква P в названии означает полиномиальную сложность алгоритма (функция сложности имеет вид ` a_0x^n + … + a_n ` , где ` x ` - длина исходных данных). Если в названии есть буква N, то оценка сложности соответствует выполнению на недетерминированной машине Тьюринга, иначе — обычной.

Почему мы выделяем именно эти два класса? Существует теорема о том, что любая программа, выполненная на недетерминированной МТ за ` t ` шагов, может быть выполнена на детерминированной за число шагов, экспоненциально зависящее от ` t ` . Приведу пример для компьютера со скоростью ` 10^6 ` операций в секунду. Рассмотрим два алгоритма: один выполняется за ` n^5 ` операций, а второй за ` 2^n ` , где ` n ` - длина входных данных. Возьмем исходные данные длиной 50. Первый алгоритм выполнится за 5 минут, для второго потребуется 35 лет. Таким же образом соотносятся и алгоритмы из классов P и NP.

Несмотря на то, что задачи из класса NP решаются гораздо дольше, до сих пор не доказано, что эти задачи невозможно решить за полиномиальное время на детерминированной МТ. Другими словами, неизвестно, совпадают ли классы P и NP. Эта задача входит в список семи задач тысячелетия. За доказательство этого факта или его опровержения предложено вознаграждение в 1 млн долларов. Класс NP содержит подмножество наиболее трудных задач, которые называются NP-полными. Это задачи, к которым можно свести любую другую задачу из класса NP за полиномиальное время. Таким образом, если для какой-либо NP-полной задачи будет найден полиномиальный алгоритм, то любая задача из класса NP может быть решена столь же быстро.

Примеры NP-полных задач

Задачи из класса NP постоянно встречаются в различных сферах жизнедеятельности: восстановление поврежденных файлов, оптимизация маршрутов, сложные вычисления в биоинформатике. Криптография открытых ключей основывается на предположении, что ` NP \ne P ` . Если найдется способ решать задачи этого класса за полиномиальное время, то многие методы защиты больше не будут иметь смысла.

Давайте рассмотрим некоторые известные NP-полные задачи. Возможно, одна из них досталась бедному Васе, а может достаться и вам.

• Задача коммивояжера. Коммивояжерами назывались торговцы в старину. Торговцу нужно обойти все города и вернуться в исходный, выбрав при этом минимальный маршрут. 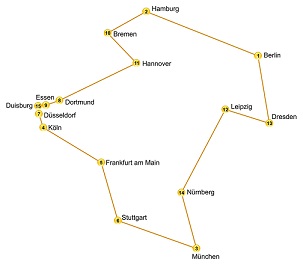Условие задачи содержит список городов и список расстояний между ними. NP-полная версия задается вопросом, есть ли маршрут, не длиннее заданного положительного числа ` K ` .
• Разбиение. Эта задача с очень простым условием. Дан набор чисел, нужно ответить на вопрос: можно ли разбить его на два подмножества с одинаковой суммой. Несмотря на простоту условия, для ее решения существуют только лишь псевдополиномиальный алгоритм. То есть задача решается за число шагов, полиномиально зависящее от числового параметра, но не от длины его записи.
• Вершинное покрытие. Многие задачи на графы являются NP-полными. 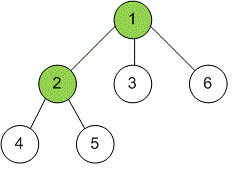Вершинным покрытием называется такое подмножество вершин графа, что у любого ребра хотя бы один конец принадлежит этому подмножеству. Задача состоит в том, чтобы определить, есть ли в заданном графе вершинное покрытие мощности ` K ` .
• Гамильтонов цикл. Еще один пример задачи на графы. Гамильтонов цикл — это замкнутый путь, который проходит через каждую вершину графа ровно по одному разу. Если переформулировать задачу коммивояжера в теории графов, то получится задача поиска Гамильтонова цикла. NP-полнота этой задачи используется в криптографии.

Метод сужения

Напоследок мы рассмотрим один из способов доказательства, что задача является NP-полной. Про многие задачи известно, что они достаточно трудны и что до сих пор нет алгоритма, который позволяет их решать за полиномиальное время. Однако вам может встретиться задача, условие которой отличается от известных NP-полных задач, но тем не менее она столь же трудна.

Метод сужения позволяет использовать известные NP-полные задачи для доказательства NP-полноты неизвестной. Для этого нужно доказать, что ваша задача принадлежит классу NP и сузить ее условие до известной NP-полной.

Разберем метод сужения на примере задачи о рюкзаке. Суть задачи в следующем: дано множество предметов с заданным весом и стоимостью. Нужно выбрать подмножество вещей с максимальной стоимостью так, чтобы они поместились в ранце с ограничением на вес. Давно известно, что эта задача NP-полная, но мы докажем это испольльзуя задачу о разбиении.

Сначала нужно доказать, что наша задача лежит в классе NP. Для этого опишем недетерминированную машину Тьюринга, которую ее решает. Первым делом МТ недетерминированно порождает всевозможные подмножества предметов. Так как это происходит независимо на различных лентах, потребуется линейное от количества предметов число шагов. Теперь осталось проверить для каждого множества, что сумма стоимостей предметов больше K, а сумма весов меньше или равна той что умещается в рюкзак. Это также требует полиномаильного числа шагов. Если найдется хоть одно такое множество, то ответ в задаче положительный.

Теперь воспользуемся задачей о разбиении для доказательства NP-полноты. Рассмотрим такую подзадачу задачи о рюкзаке, в которой вес каждого предмета совпадает с его стоимостью. Пусть ограничение на вес равно минимальной стоимости. То есть, теперь нужно найти подмножество, сумма элементов строго равна заданному числу. Если мы установим это число равным половине суммы стоимостей всех предметов, то получим в точности задачу о разбиении. Таким образом, задача о рюкзаке также NP-полная.

Заключение

Мы познакомились с теорией сложности и классом NP-полных задач. Такие задачи встречаются достаточно редко в практике рядового программиста, но нужно быть готовым ко всему. Нужно понимать, что не любой алгоритм может быть выполнен в реальные сроки. Конечно, необязательно писать машины Тьюринга для проверки, но нужно хотя бы примерно оценить его временную сложность.

Written on January 20th, 2018 by Alexey Kalina